记一记梯度下降极其优化算法
本文主要是对于An overview of gradient descent optimization algorithms的学习和理解,方便记忆
引言
梯度下降法是非常著名的优化算法之一,思想简单高效,被各种深度框架(Tensorflow、Pytorch)用做默认优化器。
梯度下降法是最小化目标函数的一种方法,利用目标函数梯度的反方向更新参数,沿着目标函数的斜面下降的方向,直到到达谷底。
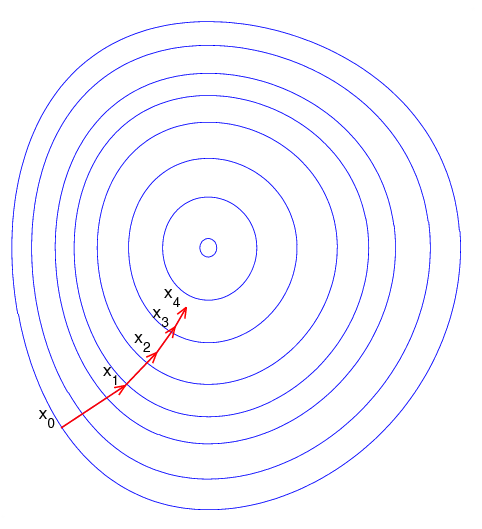
由于被广泛使用,因此在梯度下降法出了很多变种以及许多优化算法,并且他们同时都是朝着加速收敛的方向进行优化。
梯度下降极其变种
Batch gradient descent
批量梯度下降法是原始的方法,他需要对整个数据集进行计算之后才更新梯度:
$$\theta = \theta - \eta \cdot \nabla_{\eta} J(\theta)$$
用代码来表示就是这样的:1
2
3for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
批量梯度下降法可以保证模型达到全局最优,但是他的缺点多了又多:
- 梯度需要遍历整个数据集才能计算,并且只有一次参数更新
- 整个梯度更新很慢,同时数据量大到放不下内存时就不再适用该方法了
- 批量梯度下降法不使用online在更新
Stochastic gradient descent
随机梯度下降法的式子长这样子:
$$\theta = \theta - \eta \cdot \nabla_{\eta} J(\theta;x^i;y^i)$$
该方法每次计算一次样本就会更新一次梯度,用代码来表示是这样的(各个epoch之间需要对样本进行打散)1
2
3
4
5for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
SGD的特性(优势和劣势结合一起了-_-)是:
- 运行速度要比批量梯度下降法快很多
- 可以适用于在线学习
- 每次都是以高方差的方式在更新梯度,会导致损失函数的波动很大,因为波动很大,因此这个波动性使得
SGD能进入局部最优,但同时想达到最终收敛相对批量梯度下降法会更得更加复杂 - 当然有研究证明如果以一个足够小的学习率进行更新时最终也都能到达局部最优和全局最最优。
Mini-batch gradient descent
而批量梯度下降法是梯度下降法和随机梯度下降法,他每次都是对一批样本进行梯度计算之后再更新参数,
$$\theta = \theta - \eta \cdot \nabla_{\eta} J(\theta;x^{i:i+n};y^{i:i+n})$$
用代码来表示则是:1
2
3
4
5for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
代码是以
batch_size=50为例,每次都是50个样本一次更新,其他和SGD都是一样的
这种方式的好处有:
- 在更新参数时可以减少异常点的参数更新,使得收敛会更加稳定(对于
SGD而言) - 他可以充分的利用矩阵计算的优化加速(
梯度下降法样本量太多,随机梯度下降法单个样本没法使用矩阵计算),因此现在的DeepLearning算法中大部分都采用这种方式来学习
然后批量梯度下降法仍旧会存在以下问题:
- 学习率大小的问题:太小收敛会很慢,太大会很难到达最优
- 并不是所有特征的学习都是一样的,特别在稀疏数据下,每个特征的学习能力和到达最优的时间都是不一致的
因此才有了下面的各种优化算法
梯度下降优化算法
Momentum
动量优化算法可以理解为在SGD的基础上加了一个相关方向,使得SGD可以更快的到达最优点,如下图所示:
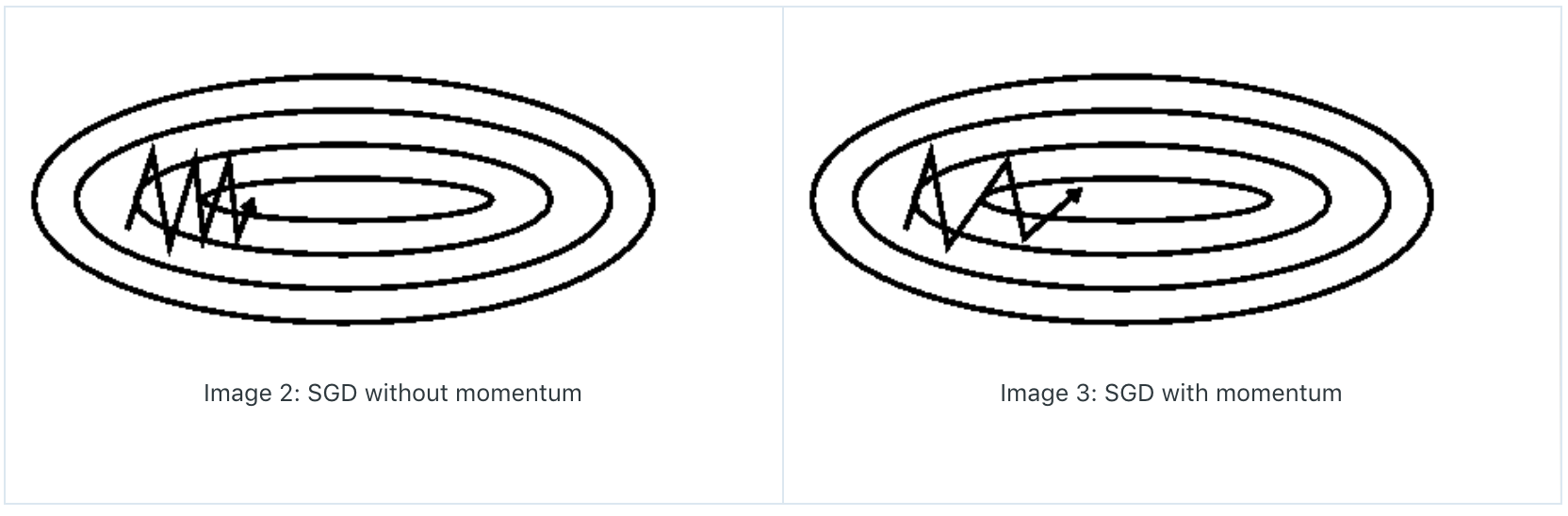
动量法主要是将历史步长的更新向量增加到当前的更新向量中:
$$v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta) \\ \theta = \theta - v_t $$
这里$v_t$就是历史梯度方向的累积,也称为方向动量,而$\gamma$称为动量项,一般都是设置为
0.9
通俗得来将,比如一个小球从小山坡上滚下来的时候,越滚会越积累动能,速度也更快的到坡低。同样在进行参数更新时:
- 与目标梯度方向相同的维度增加动量,参数更新更快,加快收敛
- 与目标梯度方向不一致的维度减少动量,降低参数更新速度,减少振荡;
而$\gamma$就像小山坡上的风阻系数,非常形象
NAG
Momentum方法虽然在参数更新时考虑了历史梯度方向,但是他在自身的梯度计算时仍为原来的方法(有波动的方向),因此Nesterov加速法(Nesterov accelerated gradient NAG)提出了在计算梯度时也加上历史的动量方向,这样每次更新的梯度也会考虑历史方向,也就是到终点就更加快了。
这里参考Momentum方法,Nesterov加速法的公式是这样的:
$$v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta-\gamma v_{t-1}) \\ \theta = \theta - v_t $$
这里和
Momentum的区别就在梯度那里的参数变成了$\theta-\gamma v_{t-1}$,而这一项正好可以让梯度朝着目标的方向计算
用图来说明应该就是这样纸了:
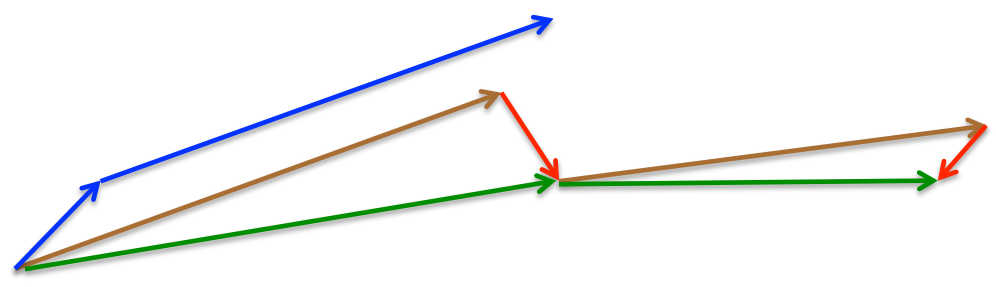
- 蓝色代表
Momentum法,他可以快速更新并且方向沿着历史梯度方向 - 而棕色和红色是代表
Nesterov方法,在后续的更新中,他的梯度会朝着最优的方向去更新(也就是红色),所以他会更快的达到最优点
AdaGrad
AdaGrad是一个可以自适应学习率的优化算法:
- 对于出现次数
较多的特征,使用小的学习率去学习 - 对于出现次数
较少的特征,使用大的学习率去学习
因此它在每一次迭代更新参数时不同的特征的参数学习率都是不一样的,在t时刻,基于对$\theta_i$计算过的历史梯度,Adagrad 修正了对每个参数对于$\theta_i$的学习率:
$$ \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{G_{t,ii} +\epsilon }} g_{t,i} $$
这边$G_{t,ii}$是一个对角矩阵,对角线上每个位置就是截止到$t$时刻的所有梯度的平方累加,$\epsilon$是为了防止除0,一般取
1e-8
用向量相乘方式可以写为
$$\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{G_t+\epsilon}} \odot g_t $$
Adagrad最大的好处就是无需手动调参,一般设置一个0.01的学习率让他自己run就行了额
不过由于$G$矩阵是平方和计算得到,所以随着训练次数的增加,$G$中的值会越来越大,导致实际的学习率会越来越小,这样当学习率逼近无限小的时候,模型的学习能力会明显不足
Adadelta
Adadelta是Adagrad的一个改进版本,他可以处理Adagrad的学习率单调递减的问题,
它将梯度的平方递归地表示替换为所有历史梯度平方的均值
$$E[g^2]_t = \gamma E[g^2]_{t-1} + (1-\gamma) g^2_t$$
这边的$\gamma$类似Momentum的动量参数,一般默认为0.9
则替换了Adagrad的对角矩阵$G$之后为,梯度的表示为
$$\Delta \theta_t = - \frac{\eta}{ \sqrt{E[g^2]_t + \epsilon}} g_t$$
同时为了保持参数的一致性(黑人问号点),这边定义了另一个指数衰减均值,该值不是梯度平方,而是参数的平方的更新
$$E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1-\gamma) \Delta \theta^2_t$$
他的更新式子为:
$$\Delta \theta_{t+1} = \theta_t - \frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t} g_t \\ \theta_t = \theta_{t-1} + \nabla \theta_{t+1}$$
这边的$RMS$是平方根的简写形式,$RMS(x) = \sqrt{(x+\epsilon)}$
因此最终Adadelta不仅解决了Adagrad的学习率消失问题,而且还不需要设置初始化的学习率
RMSProp
RMSProp是Hinton提出但是未发表的一个优化算法,他与Adadelta几乎同时发现,可以理解为它是一个Adadelta的缩减版的特例:
$$E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t \\ \theta_t = \theta_{t-1} - \frac{\eta}{ \sqrt{E[g^2]_t + \epsilon}} g_t$$
其实就是恢复了
Adadelta的初始化学习率的问题
Adam
Adam(Adaptive Moment Estimation) 是另一个比较重要学习率自适应的算法,他同时结合了Momentum的动量来快速找到梯度更新方向,同时采用RMSProp的方式来找到每个特征不同的学习率。Adam中类似动量的指数衰减均值为$m_t$,另外历史平方梯度的平均为$v_t$:
$$ m_t = \beta_1 m_{t-1} + (1- \beta_1) g_t \\ v_t = \beta_2 v_{t-1} + (1- \beta_2) g^2_t$$
$m_t$和$v_t$分别是对梯度的一阶矩(均值)和二阶矩(非确定的方差)的估计,由于他们的初始化为0向量,作者发现$\beta_1$和$\beta_2$的参数值接近于1的时候,$m_t$和$v_t$始终偏向于0 ,因此针对此问题做了矫正:
$$\hat{m}_t = \frac{m_t}{1-\beta_1^t} \\ \hat{v}_t = \frac{v_t}{1-\beta_2^t}$$
最终Adam的实际参数更新为:
$$\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v}_t}+\epsilon} \hat{m}_t $$
作者建议的参数为:$\beta_1 = 0.9$,$\beta_2 = 0.999$ , $\epsilon = 10e-8$ ,这个优化算法也是目前比较Work的一个,在DL里面非常的适用
AdaMax
针对Adam中的二阶矩的泛化形式可以表述为:$$v_t = \beta_2^p v_{t-1} + (1-\beta_2^p) |g_t|^p $$
由于$p in \{1,2\}$一般是我们认为的一范数和二范数,通过实践证明都是比较稳定的,但是当$p$变大的时这个的规范化会出现不稳定的情况。不过如果将$p$趋向于无穷大的时候,该矩的表现也是很稳定的,也就是用$u_t$来表示
$$u_t = \beta_2^\infty u_{t-1} + (1-\beta_2^\infty ) |g_t|^\infty = max(\beta_2 \cdot u_{t-1},|g_t|) $$
最后的参数更新为:
$$\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{u_t}+\epsilon} \hat{m}_t $$
这边的$u$矩不再会出现趋近于0 的情况,所以不需要再做矫正,同时建议的参数可以设置为$\beta_1 = 0.9$,$\beta_2 = 0.999$ , $\epsilon = 0.002$
Nadam
如果将Adam看做Momentum和RMSProp的组合,那其实Nadam就是NAG和RMSProp的组合的,最终眼熟的更新式子为:
$$\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{v_t}+\epsilon} ( \beta_1 \hat{m}_t + \frac{(1-\beta_1)g_t}{1-\beta_1^t}) $$
AMSGrad
Adam由于是通过累加平均二阶矩来进行参数学习率的自适应,当某些minbatch提供的信息量很大并且梯度很大时,他们会被平均掉,影响整体的训练,最终会陷入局部最优。
为了避免这种局部最优的情况,AMSGrad这个优化算法将二阶矩的矫正阶段替换为求$max$,用于增强高信息量的minbatch信息:
$$ m_t = \beta_1 m_{t-1} + (1- \beta_1) g_t
\\ v_t = \beta_2 v_{t-1} + (1- \beta_2) g^2_t
\\ \hat{v}_t = max(\hat{v}_{t-1} , v_t)
\\ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} m_t $$
虽然作者有实验证明在一些小数据集上AMSGrad的优化效果要好于Adam,但是也有好多人也实验了AMSGrad的性能比Adam更加差 -_-
总结
其实上面几个优化算法的迭代都是循序渐进并且有不少联系,归纳起来就是:
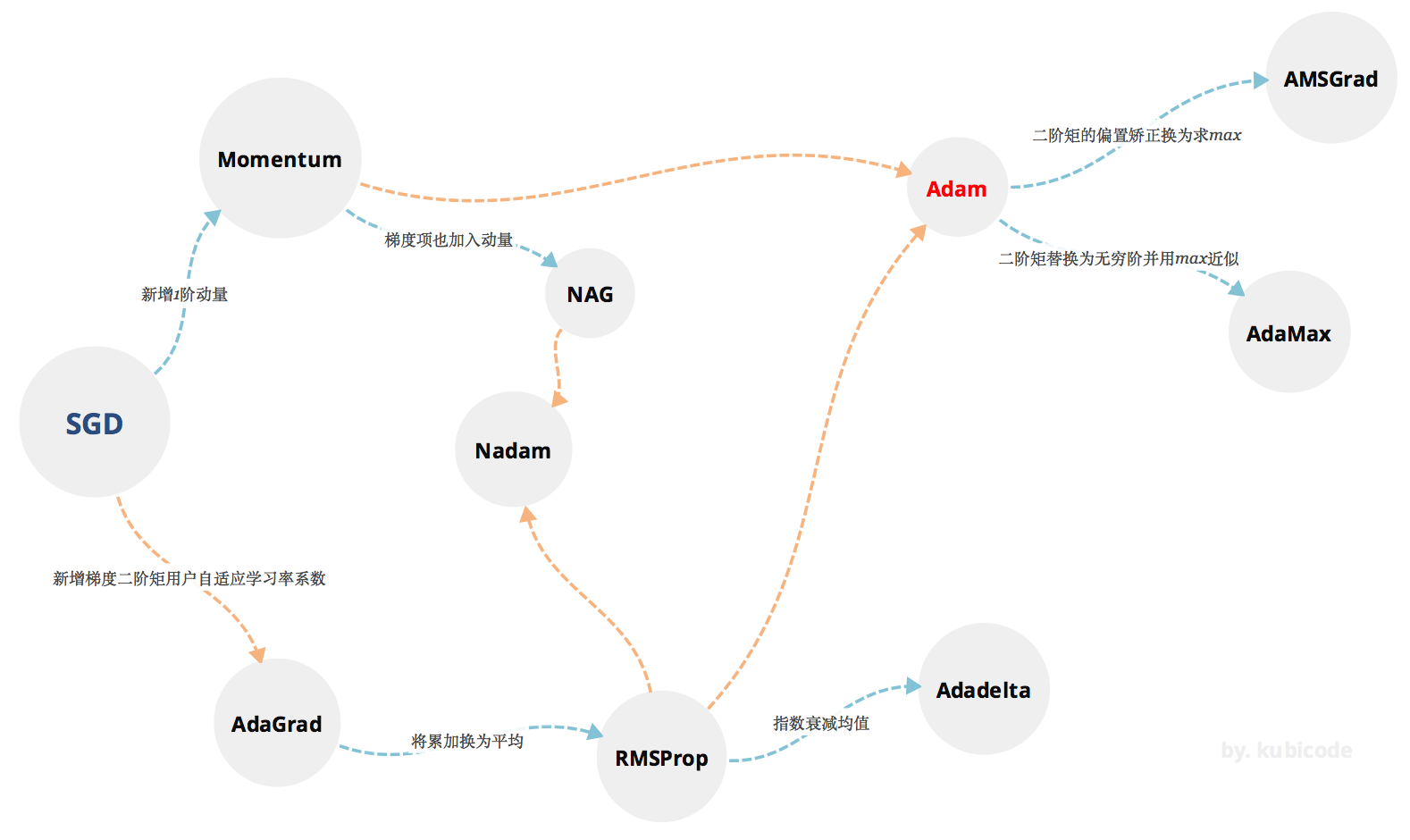
比较有创新性的应该还是Momentum和RMSProp,但是他们的结合Adam将更加普适应,他目前是各位普通炼金术士的首选

